编者按：场外期权作为资本市场中的重要金融工具，为诸多市场主体与投资者提供了灵活的风险管理和收益增强手段，也正是因为其灵活性与复杂性，导致大众缺乏对场外期权的基础认知。中证报价投教基地推出“场外期权基础知识”专栏，邀请交易商深入浅出地介绍场外期权的基本概念、风险管理和定价机制，希望能够帮助大家更加全面地了解这一复杂而高效的金融工具。

作者：东方财富证券证券投资总部

说起波动率模型，我们往往会想到类似ARCH和GARCH这种自回归条件异方差模型。这类模型虽然一定程度上揭示了波动率的结构特征，但只用到了资产本身的信息。

在期权的语境下，所谓的波动率模型往往需要和期权价格的变动结合起来，因此还是沿着隐含波动率的思路，只不过相较于BS模型放松了更多假设。接下来介绍的局部波动率模型和随机波动率模型（SVI，SABR，Heston），就是这类模型中比较常见和常用的几种。

▍局部波动率模型[1]

在BS模型中，资产价格被假设为恒定波动率的几何布朗运动。从理论上来说，这一波动率不应随着到期时间和执行价格的变化而变化，但是这和市场观察到的波动率微笑、倾斜并不相符。

为了更加准确地刻画波动率的这种特征，一个自然的想法是假设波动率是价格和时间的确定性函数，即随着时间推移和价格变化，波动率大小也会改变。而且这里的波动率只是代表了某个时刻、某个价格下的瞬时波动状态，从理论上来说和其他时刻、其他价格没有关系，所以它是“局部”的。

▍SVI模型[2]

SVI模型是一种参数化的波动率建模形式。通俗来讲，参数化就是指整个模型的构建过程没有直接的市场含义，只有经验的提炼和规律的总结。原始SVI模型的具体形式如下：

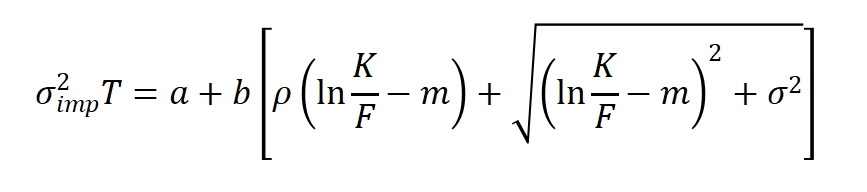
从模型的介绍中可以看得出SVI的思路：它根本不关心BS的假设，也不关心随机分析的结果，只关心期权的隐含波动率能不能用一个数学公式拟合出来。SVI虽然过程简单粗暴，但由于计算便捷，输出直观，在期权交易中运用广泛。

▍SABR[3]和Heston[4]模型

SABR模型和Heston模型的想法有一些共通之处，即除了对标的价格的变动进行建模之外，还对价格的波动率进行了建模。其中，SABR模型假设波动率本身服从几何布朗运动（左图），而Heston模型假设波动率服从带有均值回归特性的随机过程（右图）。为了更直观地体现均值回归的特点，右图中的波动率均值设置为21%，而起始点是20%，所以可以看到波动率中枢比较明显的上移，最后停留在21%附近的位置。

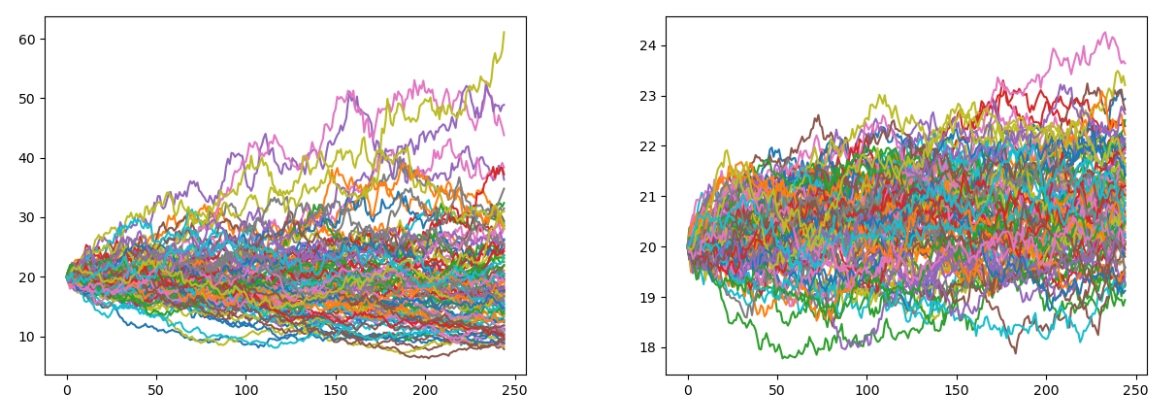
建模思想虽然不复杂，但是模型的求解还是比较困难的。目前SABR模型可以得到隐含波动率的近似解，而Heston模型则只能得到关于香草期权价格的半显示解。尽管如此，比起BS模型以及前述两种波动率模型，SABR和Heston模型对现实世界的刻画更加细节，因此也被广泛使用。

【免责声明】本文信息仅用于投资者教育之目的，不构成对投资者的任何投资建议，投资者不应当以该等信息取代其独立判断或仅根据该等信息作出决策。本文信息力求准确可靠，但对这些信息的准确性或完整性不作保证，亦不对因使用该等信息而引发或可能引发的损失承担任何责任。