编者按：场外期权作为资本市场中的重要金融工具，为诸多市场主体与投资者提供了灵活的风险管理和收益增强手段，也正是因为其灵活性与复杂性，导致大众缺乏对场外期权的基础认知。中证报价投教基地推出“场外期权基础知识”专栏，邀请交易商深入浅出地介绍场外期权的基本概念、风险管理和定价机制，希望能够帮助大家更加全面地了解这一复杂而高效的金融工具。

作者：东方财富证券证券投资总部

到目前为止，我们从场外期权合约，讲到场外期权价值，再到场外期权的风险对冲，从投教的角度讲，实际上已经完成了对场外期权基础知识的介绍。在最后的几篇文章中，我们来聊一聊场外期权交易商的核心技术：期权定价。

目前来看，学术界和市场上流行的期权定价方法主要有解析解、树方法、蒙特卡洛模拟法、有限差分法以及数值积分法等。

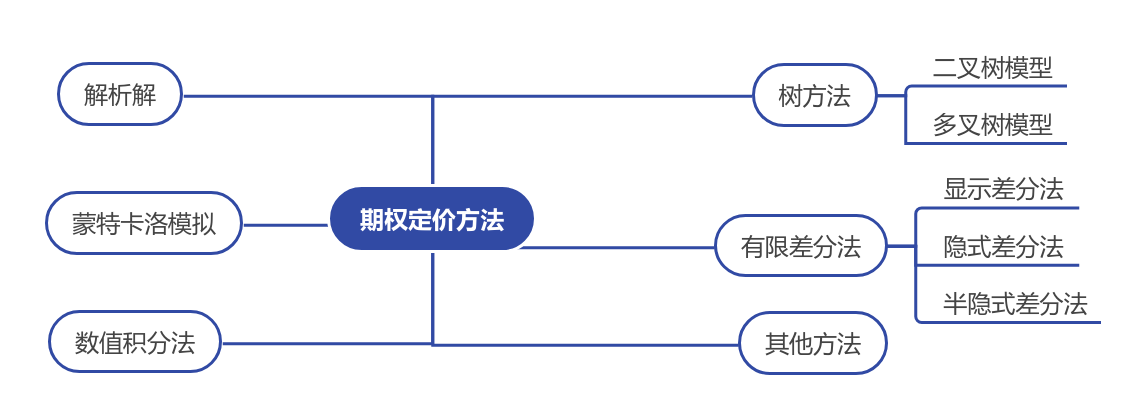
完整的期权定价涉及很多数学公式，本质上并不适合作为“基础知识”投教的内容，因此我们略去了绝大部分的数学公式，尽量从直观上把几种常用的定价思想讲清楚。

▍现金流贴现

在推导BS公式时，最常见的做法就是从“无套利”入手——正如在“期权定价公式”一章中提到的那样。但在使用数值方法对期权进行定价时，我们往往从“风险中性[1]”的角度去理解定价模型。

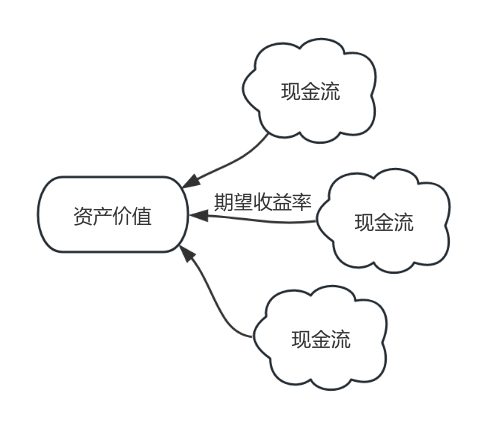
对金融有基本了解的投资者一定接触过“现金流贴现”的思想——一个资产现在的价值等于其未来现金流的现值。这一思想直白到用下面这个一看就懂的公式就可以概括：

资产价值×（1+投资者的期望收益率）=未来现金流的期望

也就是说，在这个模型下，求解一个资产的价值只需要知道两样东西（如下图）：一个是投资者的期望收益率，另一个是未来现金流的期望。框架是简单的，不过现实情况是，这两者的获取并非易事，对期权来讲更是如此。鉴于此，研究者们“抛开现实情况不谈”，在一个假想的风险中性世界中导出了期权的价格。

▍风险中性

风险中性假设了这样一个世界：这里的人对风险既不害怕也不偏爱，只关心资产收益的期望，而不会因为风险要求额外补偿。在这个世界中，所有资产的期望收益都等于无风险利率，因为人们一旦发现期望收益高的资产，就会蜂拥而至，从而导致该资产的收益下降——最终各资产收益率在无风险利率附近达到均衡。

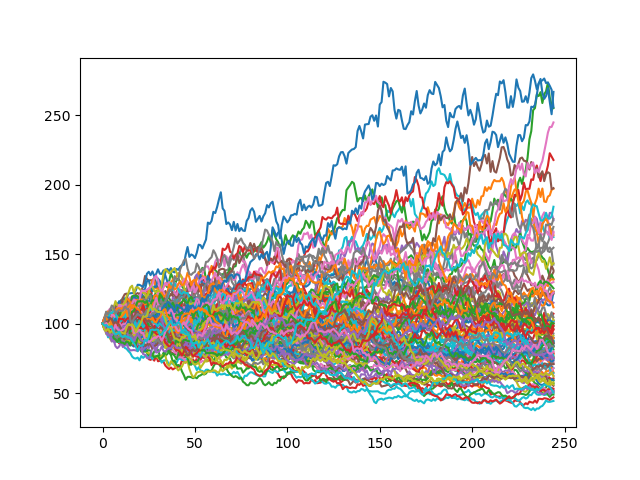
很显然，在风险中性世界中，投资者的期望收益率是确定的，那么期权未来现金流的期望是确定的吗？这里就需要回顾一下我们在“期权定价公式”一章中介绍的几何布朗运动了。如下图所示，几何布朗运动假定每一步的收益率都服从正态分布，因而使股票价格服从对数正态分布。在几何布朗运动的假设下，我们如果知道资产收益率的期望和波动率，那么很容易用一个数学公式表达出资产价格的最终概率分布。因此，期权未来现金流的期望其实也是确定的。

最后只剩一个问题：为什么“假装风险中性”能算出正确价格？我们假设这样一种情况：一款盲盒有50%的概率开出20元的公仔，有50%概率开出40元的公仔，它的期望收益是30元。但市场上人们对于盲盒的偏好是不同的，风险厌恶者觉得盲盒有风险，只愿出25元，而风险偏好者愿意出35元。在市场流动性极好、没有买卖成本的理想市场，这款盲盒应该怎么定价？

实际定价只能是30元——如果定价低于30元，套利者会大量买入转卖赚差价，抬高价格；如果定价高于30元，套利者会做空压低价格，最终市场价稳定在30元——和风险中性世界的定价相同。

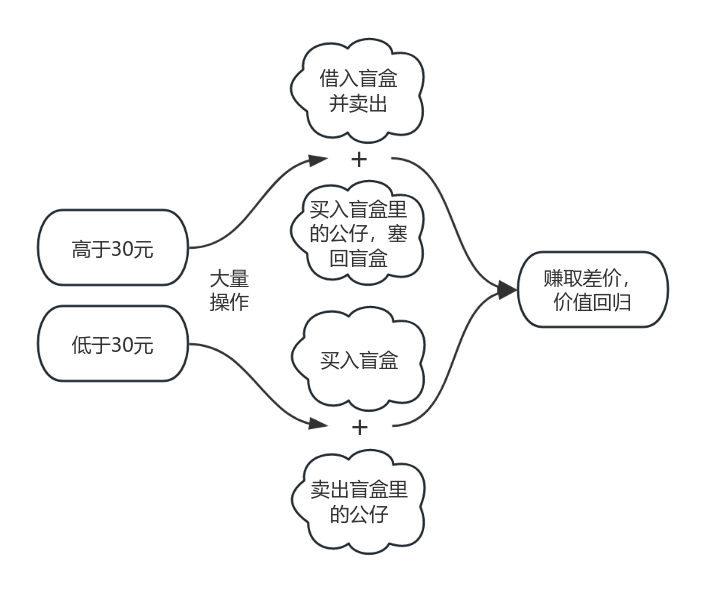
当然，现实中一定是存在交易摩擦的，比如做空限制。具体到盲盒这个商品上，上图中“借入盲盒”这一举动就稍稍有点脱离现实了，至于再把公仔塞回盲盒里，更属于痴人说梦。但是，当你把盲盒换成流动性更好，交易方式更加自由的金融产品，这种套利则未必不能实现。

最后总结一下风险中性定价的思路：在风险中性世界中，我们把无风险利率同时当做投资者和标的的期望收益率，在几何布朗运动的假设下求出标的的未来价格分布，据此得到期权未来现金流的期望，最后使用期望收益率进行贴现，得到风险中性价格。而在市场满足无套利的情况下，风险中性价格就是现实中期权的理论价格。

【免责声明】本文信息仅用于投资者教育之目的，不构成对投资者的任何投资建议，投资者不应当以该等信息取代其独立判断或仅根据该等信息作出决策。本文信息力求准确可靠，但对这些信息的准确性或完整性不作保证，亦不对因使用该等信息而引发或可能引发的损失承担任何责任。